Latihan Soal Dan Rumus Perbandingan Vektor Matematika - Setiap besaran skalar seperti temperature, tekanan, massa, dan sebagainya selau dikaitkan dengan suatu bilangan yang merupakan nilai dari besaran itu. Untuk besaran vektor, di samping mempunyai nilai, ia juga mempunyai arah. Misalnya, pada gerakan angin, selain disebutkan lajunya, disebutkan juga arahnya, seperti 20km/jam dengan arah timur laut.
Definisi vektor dan skalar :
1. Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :
Dimana adalah vektor satuan.
adalah vektor satuan.
2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




3. Vektor Satuan
Vektor satuan adalah adalah vektor yang panjangnya satu satuan. Jika vektor maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah:

4. Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor

Contoh :
Diketahui vektor Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar

b. Cross Product
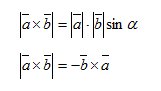







d. Rumus Pembagian


Contoh : Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili adalah :
adalah :
Jawab :
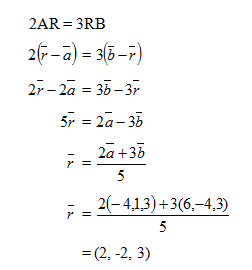

Definisi vektor dan skalar :
- Vektor : segmen garis berarah yang mempunyai besaran. Jadi, vektor adalah besaran yang mempunyai arah, misalnya : kecepatan, momen, gaya, percepatan, berat, dll.
- Skalar : suatu besaran yang tidak mempunyai arah. Misalnya, panjang, luas, jarak, ,suhu, dll.
1. Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :

Dimana
 adalah vektor satuan.
adalah vektor satuan. 2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




3. Vektor Satuan
Vektor satuan adalah adalah vektor yang panjangnya satu satuan. Jika vektor
 maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah: 
4. Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor

Contoh :
Diketahui vektor
 Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar

b. Cross Product
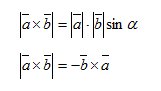







d. Rumus Pembagian


Contoh : Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili
 adalah :
adalah : Jawab :
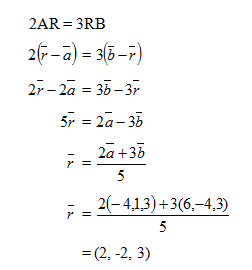

Contoh Latihan Soal Perbandingan Vektor
1. Gambarlah garis AB yang panjangnya 6 cm. Titik C adalah titik pada AB. Tandailah letak titik C sedemikian sehingga :
a. AC : CB = 2 : 1
b. AC : CB = 3 : 1
c. AC : CB = 3 : -2
d. AC : CB = 1 : -3
2. Tentukan koordinat C jika :
a. A(3,2), B(9,5) dan AC : CB = 2 : 1
b. A(-1,-3), B(7,5) dan C titik tengah dari AB
c. A(-3,-2), B(7,3) dan AC : CB = 3 : 2
3. R adalah titik pada perpanjangan PQ. Tentukan koordinat R jika :
a. P(2,1), Q(4,7) dan PR : RQ = 3 : -2
b. P(-1,-2), Q(4,0) dan PR : RQ = -2 : 1
4. M adalah titik pada garis PQ. Tentukan koordinat M jika :
a. P(1,0,2), Q(5,4,10) dan PM : MQ = 3 : 1
b. P(-3,-2,-1), Q(0,-5,2) dan PM : MQ = 4 : -3
5. Titik sudut segitiga ABC adalah A(6,-9,-3), B(2,3,0) dan C(3,5,2). T adalah titik potong garis berat dari B ke sisi AC. Tentukan koordinat titik T!
Semoga dengan postingan diatas yang berjudul Latihan Soal Dan Rumus Perbandingan Vektor Matematika dapat bermanfaat untuk sobatku semuanya yang sedang mencari beberapa contoh soal perbandingan vektor ataupun beberapa rumus rumus dari perbandingan vektor matematika ini. Dan jangan lupa untuk share postingan ini kepada teman kalian yang sedang membutuhkan informasi dari artikel ini, dan cobalah untuk share di facebook ataupun media social lainnya.

Tulisannya sangat bermanfaat untuk tugas-tugas saya. terima kasih :) sukses selalu
ReplyDelete